Ο διαγωνισμός 1Γ/2024 ήταν από τους πρώτους που έφεραν τους υποψηφίους αντιμέτωπους με τη νέα πραγματικότητα των ηλεκτρονικών εξετάσεων του ΑΣΕΠ. Μαζί με τους διαγωνισμούς για διοικητές και υποδιοικητές των Υγειονομικών Περιφερειών, εμφανίστηκαν για πρώτη φορά παραγωγικοί και επαγωγικοί συλλογισμοί. Ήταν μια ξεκάθαρη στροφή στη λιγότερη αποστήθιση και στη περισσότερη σκέψη.
Παρόλα αυτά, η συμμετοχή στον 1Γ/2024 ήταν περιορισμένοι όπως λίγες ήταν και οι θέσεις. Έτσι, ο τρόπος σκέψης που απαιτούσαν αυτά τα νέα τεστ δεν έγινε ευρέως κατανοητός. Λίγους μήνες αργότερα, όμως, ο 1Γ/2025, ο Δεύτερος Πανελλήνιος Γραπτός Διαγωνισμός του ΑΣΕΠ, με χιλιάδες θέσεις εργασίας και ακόμα περισσότερους υποψηφίους, έκανε τους συλλογισμούς μέρος της καθημερινής μας προετοιμασίας. Πλέον, δεν υπάρχει υποψήφιος που να μην έχει έρθει σε επαφή με αυτού του τύπου τις ερωτήσεις.
Σήμερα θα επιστρέψουμε λίγο πίσω, για να δούμε τους αριθμητικούς συλλογισμούς του 1Γ/2024, οι οποίοι είχαν εμφανιστεί για πρώτη φορά ήδη στον 2Γ/2022. Τότε, οι εξετάσεις ήταν δια ζώσης, γραπτές και ταυτόχρονες, σε σχολεία σε όλη τη χώρα. Το πλαίσιο ήταν διαφορετικό, αλλά οι απαιτήσεις σε λογική σκέψη ήταν ήδη εκεί.
Πάμε λοιπόν, να δούμε το παράδειγμα που είχε δώσει τότε το ίδιο το ΑΣΕΠ, και στη συνέχεια να περάσουμε σε πρακτική εξάσκηση, με ακόμα περισσότερα ερωτήματα, ώστε να μάθουμε όχι απλώς τη σωστή απάντηση, αλλά τον τρόπο σκέψης πίσω από αυτήν.
Παράδειγμα (1Γ/2024)
Μελετήστε την ακόλουθη αριθμητική σειρά και βρείτε ποιος αριθμός συμπληρώνει καλύτερα τη σειρά και αντικαθιστά το ερωτηματικό (?). Επιλέξτε τη σωστή απάντηση από τις πέντε (5) εναλλακτικές απαντήσεις (Α, Β, Γ, Δ, Ε) που σας δίνονται ακριβώς από κάτω.
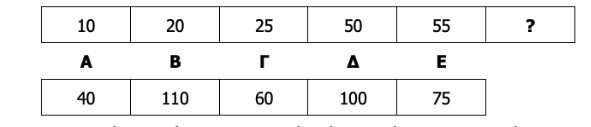
Στο ανωτέρω παράδειγμα, η σωστή απάντηση είναι το Β, δηλαδή 110.
Επεξήγηση σωστής απάντησης: Για να βρούμε ποιος αριθμός συμπληρώνει ορθά τη σειρά και αντικαθιστά το ερωτηματικό (?), το οποίο, σε αυτήν την περίπτωση, βρίσκεται στο τέλος της σειράς, χρειάζεται να αναγνωρίσουμε τις μαθηματικές σχέσεις μεταξύ των προηγούμενων αριθμών, θεωρώντας τη σειρά από τα αριστερά προς τα δεξιά: 10, 20, 25, 50, 55, ?. Μελετώντας αυτήν την ακολουθία αριθμών καταλαβαίνουμε ότι οι αριθμοί αλλάζουν σύμφωνα με το εξής μοτίβο: 10 Χ 2 = 20 + 5 = 25 Χ 2 = 50 + 5 = 55 Χ 2 = 110. Άρα, η σωστή απάντηση είναι το 110, δηλαδή η επιλογή Β.
Παρατηρούμε στο παραπάνω παράδειγμα ότι οι αριθμοί δεν αυξάνονται γραμμικά ούτε ακολουθούν μια απλή αριθμητική ή γεωμετρική πρόοδο. Αντίθετα, εφαρμόζονται διαδοχικά δύο διαφορετικές πράξεις, πρώτα πολλαπλασιασμός επί 2 και έπειτα πρόσθεση 5. Αυτό δείχνει ότι ο υποψήφιος οφείλει να ελέγχει αν το μοτίβο «σπάει» σε περισσότερα του ενός βήματα.
Επίσης, παρατηρούμε ότι το ΑΣΕΠ περιμένει από τον υποψήφιο να διαβάσει τη σειρά με κατεύθυνση, από τα αριστερά προς τα δεξιά, και να ελέγξει αν το μοτίβο επαναλαμβάνεται με συνέπεια. Δεν αρκεί να κοιτάξει κανείς τις διαφορές ή τις αναλογίες πρόχειρα, απαιτείται συστηματική παρατήρηση της σχέσης κάθε αριθμού με τον επόμενο.
Τέλος, αυτό το παράδειγμα δείχνει ότι αυτού του είδους οι αριθμητικοί συλλογισμοί (=αριθμητική ακολουθία) δεν είναι θέμα τύπων, αλλά θέμα μεθόδου. Αν ο υποψήφιος εντοπίσει το μοτίβο (Χ2, +5), η λύση προκύπτει αυτόματα. Άρα, αυτό που αξιολογείται δεν είναι η αριθμητική ικανότητα καθαυτή, αλλά η ικανότητα αναγνώρισης επαναλαμβανόμενων κανόνων, που αποτελεί βασικό στοιχείου του τρόπου εξέτασης αυτών των αριθμητικών συλλογισμών.
Μία αριθμητική ακολουθία είναι μια ταξινομημένη ακολουθία αριθμών που είναι διατεταγμένοι σύμφωνα με έναν συγκεκριμένο μαθηματικό κανόνα ή μοτίβο. Κάθε αριθμός της σειράς σχετίζεται με τους άλλους μέσω συνεπών πράξεων όπως πρόσθεση, αφαίρεση, πολλαπλασιασμός, διαίρεση, εκθέτες ή πιο σύνθετες σχέσεις.
Οι αριθμητικές ακολουθίες είναι ένα θέμα που τίθεται συχνά στους αριθμητικούς συλλογισμούς. Υπάρχουν δύο βασικά είδη ερωτήσεων που τίθενται:
- Σειρά αριθμών και ερωτηματικό: δίνεται μια ακολουθία με έναν ή ακόμα και περισσότερους αριθμούς να λείπουν και πρέπει να βρείτε τον σωστό αριθμό που ταιριάζει στο μοτίβο.
- Σειρά με λάθος αριθμούς: δίνεται μια πλήρης ακολουθία, αλλά ένας αριθμός είναι λανθασμένος και πρέπει να τον εντοπίσετε και, σε ορισμένες περιπτώσεις, να τον διορθώσετε.
Πάμε τώρα να επιλύσουμε κάποια ερωτήματα για να δούμε αν έχουμε «πιάσει» τη λογική και κυρίως αν μπορεί να αναγνωρίσει ο εκάστοτε υποψήφιος το μοτίβο:
Ερώτημα 1ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
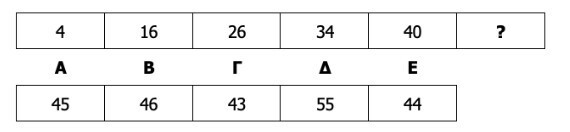
Επεξήγηση σωστής απάντησης: Για να σκεφτεί σωστά ο υποψήφιος, ξεκινά από το πιο απλό και ασφαλές βήμα, κοιτάζει τις διαφορές ανάμεσα στους διαδοχικούς όρους (γιατί σε πολλές σειρές το μοτίβο κρύβεται εκεί). Η σειρά είναι: 4, 16, 26, 34, 40, ?. Υπολογίζουμε τις διαφορές: 16 – 4 = +12, 26 – 16 = +10, 34 – 26 = +8, 40 – 34 = +6. Τώρα παρατηρούμε το μοτίβο των διαφορών: 12, 10, 8, 6. Κάθε φορά μειώνονται κατά 2. Άρα η επόμενη διαφορά πρέπει να είναι +4. Επομένως, ο επόμενος όρος είναι 40 + 4 = 44. Άρα, η σωστή απάντηση είναι η επιλογή Ε.
Ερώτημα 2ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
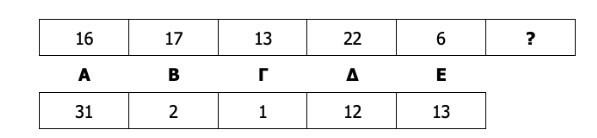
Επεξήγηση σωστής απάντησης: Για να βρει τη σωστή απάντηση, ο υποψήφιος δεν κοιτάζει πρώτα τους ίδιους τους αριθμούς, αλλά πώς αλλάζουν από τον έναν στον επόμενο. Παρατηρεί ότι οι μεταβολές δεν είναι τυχαίες, πότε ο αριθμός αυξάνεται και πότε μειώνεται, άρα κάτι εναλλάσσεται. Αν υπολογίσει τις διαφορές, βλέπει ότι αυτές είναι διαδοχικά +1, -4, +9 και -16. Οι αριθμοί αυτοί δεν είναι οποιοιδήποτε είναι τετράγωνα φυσικών αριθμών (12, 22, 32, 42) και μάλιστα εμφανίζονται με εναλλαγή προσήμου. Το μοτίβο λοιπόν είναι αύξηση κατά τετράγωνο, μετά μείωση κατά τετράγωνο, και αυτό συνεχίζεται. Ακολουθώντας το ίδιο σκεπτικό, η επόμενη μεταβολή πρέπει να είναι +25 (52). Προσθέτοντας το 25 στον τελευταίο αριθμό της σειράς (6), προκύπτει το 31. Επομένως, η σωστή απάντηση είναι η επιλογή Α.
Ερώτημα 3ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
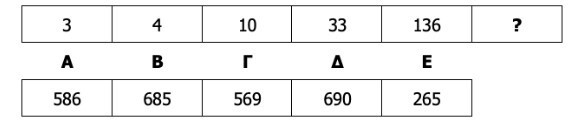
Επεξήγηση σωστής απάντησης: Για να εντοπίσει το μοτίβο, ο υποψήφιος εξετάζει πώς προκύπτει κάθε αριθμός από τον προηγούμενο. Παρατηρεί ότι δεν πρόκειτια για απλή αύξηση, αλλά για συνδυασμό πράξεων που επαναλαμβάνεται με συνέπεια. Κάθε όρος προκύπτει αν ο προηγούμενος αριθμός πολλαπλασιαστεί με έναν αυξανόμενο φυσικό αριθμό και στη συνέχεια προστεθεί ο ίδιος αυτός αριθμός. Συγκεκριμένα, πρώτα πολλαπλασιάζουμε με 1 και προσθέτουμε 1, μετά με 2 και προσθέτουμε 2, στη συνέχεια με 3 και προσθέτουμε 3 και έπειτα με 4 και προσθέτουμε 4. Ακολουθώντας το ίδιο σκεπτικό, ο επόμενος αριθμός πρέπει να προκύψει από τον πολλαπλασιασμό του 136 με 5 και την πρόσθεση του 5, που μας δίνει το 685. Επομένως, η σωστή απάντηση είναι η επιλογή Β.
Ερώτημα 4ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;

Επεξήγηση σωστής απάντησης: Για να το βρει ο υποψήφιος, καλό είναι να ψάξει κανόνα που επαναλαμβάνεται από όρο σε όρο, όχι απλώς διαφορές. Εδώ φαίνεται ότι κάθε φορά πολλαπλασιάζουμε τον προηγούμενο αριθμό με έναν αύξοντα αριθμό (1, 2, 3, 4, …) και μετά αφαιρούμε τον αμέσως επόμενο (2, 3, 4, 5, …). Δηλαδή, 6 Χ 1 -2 = 4 Χ 2 – 3 =5 Χ 3 – 4 = 11 Χ 4 – 5 = 39. Συνεχίζοντας με τον ίδιο κανόνα: 39 Χ 5 – 6 = 189. Άρα, η σωστή απάντηση είναι η επιλογή Γ.
Ερώτημα 5ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
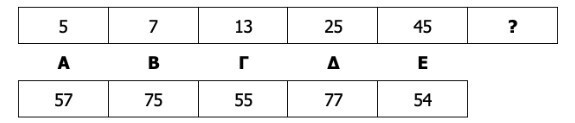
Επεξήγηση σωστής απάντησης: Για να προσεγγίσει σωστά αυτή τη σειρά, ο υποψήφιος ξεκινά παρατηρώντας πώς μεταβάλλεται κάθε αριθμός σε σχέση με τον προηγούμενο. Δεν αρκεί να δει ότι οι αριθμοί αυξάνονται, χρειάζεται να ελέγξει αν η αύξηση ακολουθεί κάποιο επαναλαμβανόμενο μοτίβο. Υπολογίζοντας τις διαφορές μεταξύ διαδοχικών όρων, προκύπτουν οι τιμές 2, 6, 12 και 20. Αυτές οι διαφορές δεν είναι τυχαίες, αλλά αυξάνονται με συγκεκριμένο τρόπο. Αν εξετάσει κανείς πιο προσεκτικά τις διαφορές, θα διαπιστώσει ότι καθεμιά προκύπτει ως γινόμενο δύο διαδοχικών φυσικών αριθμών: 1 Χ 2, 2 Χ 3, 3 Χ 4 και 4 Χ 5. Το μοτίβο, λοιπόν, δεν βρίσκεται στους ίδιους τους αριθμούς της σειράς, αλλά στις μεταβολές τους. Ακολουθώντας την ίδια λογική, η επόμενη διαφορά πρέπει να είναι 5 Χ 6, δηλαδή 30. Προσθέτοντας αυτή τη διαφορά στον τελευταίο γνωστό αριθμό της σειράς, έχουμε 45 + 30 = 75. Έτσι καταλήγουμε στο συμπέρασμα ότι ο αριθμός που συμπληρώνει σωστά τη σειρά είναι το 75, που αντιστοιχεί στη σωστή επιλογή Β.
Ερώτημα 6ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
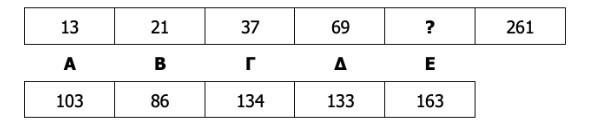
Επεξήγηση σωστής απάντησης: Για να βρει τη λύση, ο υποψήφιος εξετάζει πώς αλλάζει κάθε αριθμός σε σχέση με τον προηγούμενο και όχι απλώς το μέγεθός του. Υπολογίζοντας τις διαφορές μεταξύ των διαδοχικών όρων, παρατηρεί ότι από το 13 στο 21 η αύξηση είναι 8, από το 21 στο 37 είναι 16 και από το 37 στο 69 είναι 32. Οι διαφορές αυτές δεν είναι τυχαίες, ακολουθούν ξεκάθαρο μοτίβο διπλασιασμού. Ακολουθώντας την ίδια λογική, η επόμενη αύξηση πρέπει να είναι διπλάσια της προηγούμενης, δηλαδή 64. Προσθέτοντας το 64 στο 69, προκύπτει ο αριθμός 133. Ο έλεγχος επιβεβαιώνει το μοτίβο, αφού από το 133 στο 261 η διαφορά είναι 128, δηλαδή πάλι διπλάσια από την προηγούμενη. Επομένως, ο αριθμός που συμπληρώνει σωστά τη σειρά είναι το 133. Άρα, η απάντηση είναι η επιλογή Δ.
Ερώτημα 7ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
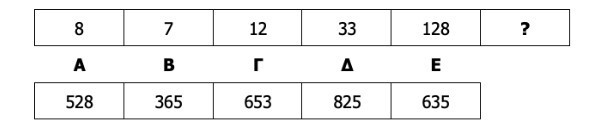
Επεξήγηση σωστής απάντησης: Για να βρει ο υποψήφιος το μοτίβο, κοιτάζει αν κάθε όρος προκύπτει από τον προηγούμενο με έναν κανόνα που επαναλαμβάνεται. Εδώ βλέπουμε ότι κάθε φορά πολλαπλασιάζουμε τον προηγούμενο αριθμό με 1, μετά με 2, μετά με 3, μετά με 4 και στη συνέχεια αφαιρούμε τον ίδιο αριθμό: 8 Χ 1 – 1 = 7 Χ 2 – 2 = 12 Χ 3 – 3 = 33 Χ 4 – 4 = 128. Άρα, συνεχίζουμε με τον ίδιο τρόπο 128 Χ 5 – 5 = 635. Άρα, η σωστή απάντηση είναι η επιλογή Ε.
Ερώτημα 8ο
Τι πρέπει να τοποθετηθεί στη θέση του ερωτηματικού (?) στην ακόλουθη αριθμητική σειρά;
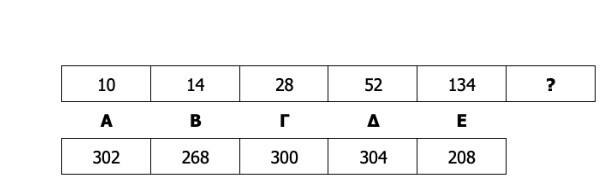
Επεξήγηση σωστής απάντησης: Για να εντοπίσει το μοτίβο, ο υποψήφιος παρατηρεί ότι κάθε όρος της σειράς προκύπτει από τον προηγούμενο με δύο συνδυασμένες πράξεις που επαναλαμβάνονται με συνέπεια. Συγκεκριμένα, κάθε φορά ο αριθμός πολλαπλασιάζεται με έναν διαδοχικά αυξανόμενο φυσικό αριθμό και στη συνέχεια αφαιρείται ένας ζυγός αριθμός, ο οποίος αυξάνεται σταθερά. Πιο αναλυτικά, ο πολλαπλασιαστής αυξάνεται κατά μία μονάδα κάθε φορά (Χ3, Χ4, Χ5, Χ6), ενώ ο αριθμός που αφαιρείται αυξάνεται ανά δύο (-2, -4, -6, -8). Ακολουθώντας αυτό το σταθερό μοτίβο, από το 52 προκύπτει ο επόμενος όρος της σειράς ως 52Χ6-8, που ισούται με 304. Επομένως, ο αριθμός που συμπληρώνει σωστά τη σειρά είναι η επιλογή Δ.