Οι αριθμητικές ακολουθίες δεν είναι απλώς μια σειρά αριθμών, είναι ένας μικρός γρίφος λογικής που δοκιμάζει την ικανότητα του υποψηφίου να αναγνωρίζει μοτίβα και να σκέφτεται μεθοδικά. Αν το μοτίβο εντοπιστεί έγκαιρα, η λύση προκύπτει σχεδόν αυτόματα. Αν όχι, ο χρόνος χάνεται και η ερώτηση γίνεται παγίδα.
Δεν είναι τυχαίο ότι οι αριθμητικές ακολουθίες εμφανίστηκαν για πρώτη φορά στις γραπτές δοκιμασίες του πρώτου πανελλήνιου γραπτού διαγωνισμού του ΑΣΕΠ το 2023 (2Γ/2022) και επανήλθαν έναν χρόνο αργότερα στον γραπτό διαγωνισμό των δασοπόνων (1Γ/2024). Η επανάληψή τους επιβεβαιώνει ότι αποτελούν πλέον σταθερό τύπο ερωτήσεων στις σύγχρονες διαγωνιστικές εξετάσεις.
Αριθμητική ακολουθία είναι μια σειρά αριθμών που ακολουθεί κάποιο λογικό μοτίβο.
Οι υποψήφιοι καλούνται συνήθως:
- Να βρουν τον αριθμό που λείπει,
- Να εντοπίσουν τον λανθασμένο όρο ή
- Να προβλέψουν τον επόμενο αριθμό της σειράς.
Σε ορισμένες δηλαδή ερωτήσεις, ένας από τους όρους μπορεί να είναι σκόπιμα λάθος και ο υποψήφιος πρέπει να τον εντοπίσει, αναγνωρίζοντας τον κανόνα που διέπει τη σειρά.
Δεν υπάρχει ένα και μοναδικό μοτίβο που εφαρμόζεται παντού.
Κάθε ερώτηση μπορεί να βασίζεται σε διαφορετικό τύπο λογικής ή σε συνδυασμό κανόνων. Γι’ αυτό και οι αριθμητικές ακολουθίες δεν ελέγχουν απλώς αριθμητικές γνώσεις, αλλά κυρίως κοινή λογική, παρατηρητικότητα και ικανότητα συλλογισμού.
Η σωστή προσέγγιση είναι πάντα η ίδια:
- Ελέγχεις πρώτα τα απλά μοτίβα
- Αν δεν «βγαίνει», προχωράς στα πιο σύνθετα
- Δεν κολλάς σε μία μόνο ιδέα
Με βάση τη μέχρι σήμερα εμπειρία από διαγωνισμούς, οι αριθμητικές ακολουθίες μπορούν να ταξινομηθούν στους εξής βασικούς τύπους:
1. Αριθμητική ακολουθία πρόσθεσης
Είναι μια ακολουθία όπου κάθε επόμενος αριθμός προκύπτει από την πρόσθεση μιας σταθερής τιμής (η κοινή διαφορά) στον προηγούμενο αριθμό.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 2, 6, 12, 20, ?
Α. 28
Β. 30
Γ. 32
Δ. 36
Επεξήγηση σωστής απάντησης: Η ακολουθία ακολουθεί το μοτίβο της πρόσθεσης διαδοχικών ζυγών αριθμών που μεταβάλλονται ανά 2 μονάδες:
2+4=6
6+6=12
12+8=20
Έτσι, ο επόμενος αριθμός θα είναι: 20+10=30
2. Αριθμητική ακολουθία αφαίρεσης
Είναι μια ακολουθία στην οποία βρίσκεις τον επόμενο αριθμό αφαιρώντας επανειλημμένα μια συγκεκριμένη τιμή ή ένα μεταβαλλόμενο ποσό από τον προηγούμενο αριθμό, κάτι που είναι συνηθισμένο στα λογικά παζλ και τα μαθηματικά.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 64, 58, 52, 46, ?
Α. 40
Β. 38
Γ. 42
Δ. 44
Επεξήγηση σωστής απάντησης: Η σειρά ακολουθεί το μοτίβο της αφαίρεσης ενός ίδιου ζυγού αριθμού:
64-6=58
58-6=52
52-6=46
Έτσι, ο επόμενος αριθμός θα είναι: 46-6=40
3. Αριθμητική ακολουθία πολλαπλασιασμού
Ο πολλαπλασιασμός μιας αριθμητικής ακολουθίας συνήθως σημαίνει την εύρεση μιας γεωμετρικής προόδου (πολλαπλασιασμός με τον ίδιο «κοινό λόγο») ή ενός πιο σύνθετου μοτίβου (όπως εναλλασσόμενες πράξεις ή δυνάμεις) για να βρούμε τους όρους που λείπουν ή τον επόμενο αριθμό.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 3, 9, 27, 81, ?
Α. 121
Β. 162
Γ. 243
Δ. 154
Επεξήγηση σωστής απάντησης: Η σειρά ακολουθεί το μοτίβο του πολλαπλασιασμού με το 3.
3Χ3=9
9Χ3=27
27Χ3=81
Έτσι, ο επόμενος αριθμός θα είναι: 81Χ3=243.
4. Αριθμητική ακολουθία διαίρεσης
Είναι μια ακολουθία στην οποία ο επόμενος αριθμός βρίσκεται διαιρώντας έναν όρο με έναν συγκεκριμένο αριθμό, συχνά με τον διαιρέτη να αλλάζει με προβλέψιμο τρόπο (όπως διαίρεση με 5, μετά με το 4, μετά το 3) ή να παραμείνει σταθερός, απαιτώντας αναγνώριση μοτίβου για την επίλυση.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 144, 72, 36, 18, ?
Α. 12
Β. 9
Γ. 6
Δ. 3
Επεξήγηση σωστής απάντησης: Η σειρά
ακολουθεί το μοτίβο της διαίρεσης με το 2.
144/2=72
72/2=36
36/2=18
Έτσι, ο επόμενος αριθμός θα είναι: 18/2=9.
5. Ακολουθία τετραγώνων
Μια σειρά τετραγωνικών αριθμών είναι μια ακολουθία αριθμών που σχηματίζεται πολλαπλασιάζοντας έναν ακέραιο αριθμό με τον εαυτό του. Αυτοί οι αριθμοί αντιπροσωπεύουν τις περιοχές τετραγώνων σε ακέραιες πλευρές και σχηματίζουν ένα θεμελιώδες μοτίβο στα μαθηματικά που χρησιμοποιείται πολύ συχνά.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 1, 4, 9, 16, ?
Α. 20
Β. 25
Γ. 30
Δ. 36
Επεξήγηση σωστής απάντησης:
Η ακολουθία αντιπροσωπεύει τα τετράγωνα των διαδοχικών φυσικών αριθμών.
1^2=1
2^2=4
3^2=9
4^2=16
Έτσι, ο επόμενος αριθμός της σειράς θα είναι: 5^2=25.
6. Ακολουθία κύβων
Μια σειρά αριθμών κύβων είναι μια ακολουθία αριθμών όπου κάθε όρος είναι το αποτέλεσμα του πολλαπλασιασμού ενός ακέραιου αριθμού με τον εαυτό του τρεις φορές.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 8, 27, 64, 125, ?
Α. 200
Β. 216
Γ. 256
Δ. 150
Επεξήγηση σωστής απάντησης: Η ακολουθία αντιπροσωπεύει τους κύβους των διαδοχικών φυσικών αριθμών.
2^3=8
3^3=27
4^3=64
5^3=125
Έτσι, ο επόμενος αριθμός θα είναι: 6^3=216.
7. Ακολουθία Fibonacci
Κάθε αριθμός είναι το άθροισμα των δύο προηγούμενων.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 0, 1, 1, 2, 3, 5, ?
Α. 6
Β. 7
Γ. 8
Δ. 9
Επεξήγηση σωστής απάντησης: Η ακολουθία ακολουθεί το μοτίβο της πρόσθεσης των δύο προηγούμενων αριθμών για να βρούμε τον επόμενο αριθμό.
0+1=1
1+1=2
1+2=3
2+3=5
Έτσι, ο επόμενος αριθμός θα είναι: 3+5=8.
8. Εναλλασσόμενη ακολουθία
Περιλαμβάνει μοτίβα πέρα από την απλή πρόσθεση / αφαίρεση, χρησιμοποιώντας συχνά εναλλασσόμενους όρους, πολλαπλές διασταυρούμενες ακολουθίες, λειτουργίες (πρόσθεση/αφαίρεση/πολλαπλασιασμός/διαίρεση) που αλλάζουν σε κάθε βήμα, ή σχετίζονται με γνωστές ακολουθίες όπως Fibonacci, τετράγωνα ή κύβοι.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 4, 9, 6, 11, 8, ?
Α. 7
Β. 12
Γ. 13
Δ. 9
Επεξήγηση σωστής απάντησης: Η σειρά ακολουθεί το μοτίβο της εναλλαγής μεταξύ της πρόσθεσης του 5 και της αφαίρεσης του 3.
4+5=9
9-3=6
6+5=11
11-3=8
Έτσι, ο επόμενος αριθμός θα είναι: 8+5=13.
9. Ακολουθία με μικτούς τελεστές
Μια σειρά αριθμών με μικτούς τελεστές συνδυάζει διαφορετικές μαθηματικές πράξεις (πρόσθεση, αφαίρεση, πολλαπλασιασμό, διαίρεση, τετράγωνα, κύβους) σε μια ενιαία ακολουθία ή συνυφαίνει πολλαπλά μοτίβα, για να δημιουργήσει ένα σύνθετο αριθμητικό γρίφο που απαιτεί να εντοπίσετε το συνδυασμό των κανόνων.
Παράδειγμα:
Βρείτε τον επόμενο αριθμό της ακολουθίας: 10, 22, 46, 94, 190, ?
Α. 384
Β. 382
Γ. 297
Δ. 190
Επεξήγηση σωστής απάντησης: Η σειρά ακολουθεί πολλαπλασιασμό επί 2 και μετά πρόσθεση 2.
10Χ2+2=22
22Χ2+2=46
46Χ2+2=94
94Χ2+2=190
Έτσι, ο επόμενος αριθμός θα είναι: 190Χ2+2=382.
Αναγνωρίζετε κάποιο από τα παραπάνω είδη αριθμητικών ακολουθιών που παρουσιάσαμε σήμερα στα δύο παραδείγματα του ΑΣΕΠ;
1ο παράδειγμα ακολουθίας του ΑΣΕΠ από τον 1ο Γραπτό Πανελλήνιο 2Γ/2022: (πρόσθεσης)
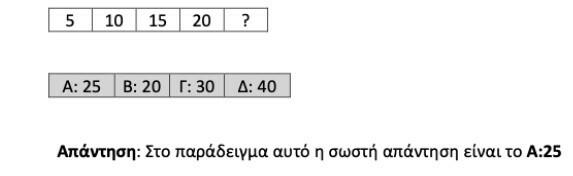
Επεξήγηση σωστής απάντησης: 5, 5+5 = 10, 10+5 = 15, 15+5 = 20, 20+5 = 25.
2ο παράδειγμα ακολουθίας του ΑΣΕΠ από τον 1Γ/2024 (ΤΕ Δασοπονίας): (πολλαπλασιασμού)
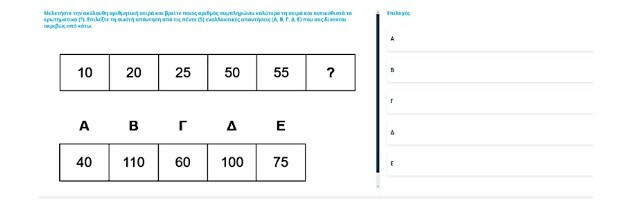
Στο ανωτέρω παράδειγμα, η σωστή απάντηση είναι το Β, δηλαδή 110.
Επεξήγηση σωστής απάντησης: Για να βρούμε ποιος αριθμός συμπληρώνει ορθά τη σειρά και αντικαθιστά το ερωτηματικό (?), το οποίο, σε αυτήν την περίπτωση, βρίσκεται στο τέλος της σειράς, χρειάζεται να αναγνωρίσουμε τις μαθηματικές σχέσεις μεταξύ των προηγούμενων αριθμών, θεωρώντας τη σειρά από τα αριστερά προς τα δεξιά: 10, 20, 25, 50, 55, ?. Μελετώντας αυτήν την ακολουθία αριθμών, καταλαβαίνουμε ότι οι αριθμοί αλλάζουν σύμφωνα με το εξής μοτίβο: 10 Χ 2 = 20, 20 + 5 = 25, 25 Χ 2 = 50, 50 + 5 = 55, 55 Χ 2 = 110.
Θα επιστρέψουμε σύντομα με πλήθος ερωτημάτων γιατί στις αριθμητικές ακολουθίες η συστηματική εξάσκηση είναι αυτή που κάνει τελικά τη διαφορά!