Η καταμέτρηση γεωμετρικών σχημάτων φαίνεται απλή, αλλά στην πράξη απαιτεί παρατηρητικότητα και συστηματική προσέγγιση. Σε αυτό το άρθρο θα αναλύσουμε πώς να προσεγγίζεις τέτοιες ασκήσεις, με μεθοδολογία, παραδείγματα και τεχνικές που θα σε βοηθήσουν να αποφύγεις λάθος απαντήσεις.
Στον 31ο Εισαγωγικό Διαγωνισμό είχε πέσει στο τεστ των γνώσεων και δεξιοτήτων μια ερώτηση στην οποία ο/η εξεταζόμενος/η είχε να μετρήσει σχήματα μέσα σε ένα σχήμα και ειδικότερα:
Ερώτηση 38
Πόσα τρίγωνα περιλαμβάνονται συνολικά στο σχήμα, αν μετρήσουμε όλα τα τρίγωνα (μικρά, μεγάλα και σύνθετα);

Α. 16
Β. 27
Γ. 30
Δ. Κανένα από τα παραπάνω
Σήμερα θα μάθουμε πώς να επιλύουμε τέτοια προβλήματα και να μην μας φοβίζουν όταν τα βλέπουμε μπροστά μας.
Θα ξεκινήσουμε από απλά σχήματα και σιγά σιγά θα μάθουμε τον τρόπο και για πιο πολύπλοκα.
Σχήμα 1ο

Εδώ έχουμε συνολικά δύο διαγώνιες και τέσσερα τρίγωνα. Οπότε ο τύπος για τον αριθμό των τριγώνων είναι 4 Χ 2 = 8. Οπότε εδώ, αν μας ρωτήσουν πόσα τρίγωνα περιλαμβάνονται μέσα στο σχήμα, θα απαντήσουμε 8 τρίγωνα.
Σχήμα 2ο
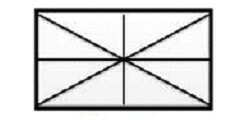
Εδώ έχουμε συνολικά δύο διαγώνιες και οκτώ τρίγωνα. Οπότε ο τύπος για τον αριθμό των τριγώνων είναι 8 Χ 2 = 16. Οπότε εδώ, αν μας ρωτήσουν πόσα τρίγωνα περιλαμβάνονται μέσα στο σχήμα, θα απαντήσουμε 16 τρίγωνα.
Σχήμα 3ο

Εδώ έχουμε δύο τετράγωνα τα οποία, όπως είδαμε παραπάνω στο σχήμα 1ο, περιέχουν 8 τρίγωνα, και, αν συνδυάσουμε και τα δύο τρίγωνα που δημιουργούνται λόγω του συνδυασμού των σχημάτων (ένα που έχει τη βάση του κάτω και ένα ανάποδο), έχουμε σύνολο τριγώνων 8 + 8 + 2 = 18 τρίγωνα.
Σχήμα 4ο
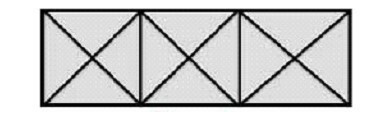
Και αυτό τώρα είναι ένα εύκολο σχήμα για εσάς για να μετρήσουμε τρίγωνα. Σύμφωνα με το σχήμα 1ο, το κάθε τετράγωνο έχει 8 τρίγωνα, και, αν μετρήσουμε και τα 4 τρίγωνα που δημιουργούνται συνδυαστικά (2 τετράγωνα που έχουν τη βάση τους προς τα κάτω και δύο ανάποδα), έχουμε σύνολο 8 + 8 + 8 + 4 = 28 τρίγωνα.
Σχήμα 5ο

Εδώ κάνουμε το εξής τρικ: μετράμε τα τρίγωνα τα εμφανή και τα προσθέτουμε μεταξύ τους. Άρα εδώ, αν μας ρωτήσουν πόσα τρίγωνα περιλαμβάνονται στο σχήμα αυτό, είναι 1 + 2 = 3 τρίγωνα. Και, πράγματι, αν το σκεφτείτε, είναι τα δύο τρίγωνα τα εμφανή και ένα που τα περικλείει και τα δύο.
Σχήμα 6ο
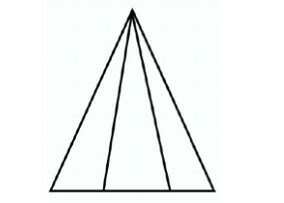
Πάμε τώρα, με τον ίδιο τρόπο όπως στο σχήμα 5ο, να επιλύσουμε και αυτό το σχήμα. Μετρήστε τώρα πόσα τρίγωνα περιλαμβάνονται μέσα στο σχήμα με τον τρόπο που μάθαμε, επομένως μετράμε τα τρίγωνα μεταξύ τους και πάλι, οπότε έχουμε 1 + 2 + 3 = 6 τρίγωνα είναι η απάντηση.
Σχήμα 7ο

Εδώ κάνουμε το ίδιο πάλι. Μετράμε τα τρίγωνα που έχουν τη βάση τους στο κάτω μέρος, δηλαδή 4 τρίγωνα, και τα προσθέτουμε μεταξύ τους προκειμένου να υπολογίσουμε πόσα τρίγωνα περιλαμβάνονται στο μεγάλο τρίγωνο, οπότε 1 + 2 + 3 + 4 = 10 τρίγωνα.
Σχήμα 8ο

Άλλο ένα τρίγωνο το οποίο έχει την ίδια λογική επίλυσης, μετράμε τα τρίγωνα που έχουν τη βάση τους στο κάτω μέρος και μετά προσθέτουμε μεταξύ τους τα τρίγωνα που μετρήσαμε ως εξής: 1 + 2 + 3 + 4 + 5 = 15 τρίγωνα.
Σχήμα 9ο
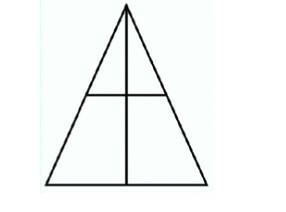
Εδώ, ως εμφανή τρίγωνα, παρατηρούμε ότι σε ένα μεγάλο τρίγωνο παρατηρούμε δύο τρίγωνα που έχουν τη βάση τους στο μεγάλο τρίγωνο και δύο μικρότερα που έχουν τη βάση τους στη μέση, οπότε κάνουμε το ίδιο με το παραπάνω σκεπτικό, αλλά πολλαπλασιάζουμε τις φορές των τριγώνων ως εξής: (1+2) Χ 2 = 3 Χ 2 = 6 τρίγωνα. Αν μας ρωτήσουν επομένως σε αυτό το μεγάλο τρίγωνο πόσα τρίγωνα περιλαμβάνονται, θα απαντήσουμε 6 τρίγωνα.
Σχήμα 10ο
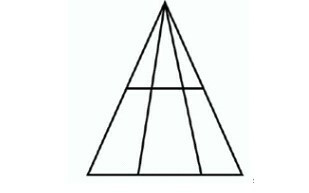
Με το ίδιο σκεπτικό όπως στο σχήμα 9ο θα επιλύσουμε και αυτό το πρόβλημα. Έχουμε 3 τρίγωνα τα οποία προσθέτουμε μεταξύ τους και μετά τα πολλαπλασιάζουμε με τις οριζόντιες γραμμές, οπότε: (1 + 2 + 3) Χ 2 = 6 Χ 2 = 12. Αν μας ρωτήσουν λοιπόν πόσα τρίγωνα περιλαμβάνονται στο μεγάλο τρίγωνο, είναι 12 τρίγωνα η απάντηση.
Σχήμα 11ο

Πάλι και εδώ μετράμε 3 τρίγωνα παρατηρώντας από τη βάση και θα τα πολλαπλασιάσουμε με τον αριθμό 3, δηλαδή όσες είναι και οι οριζόντιες γραμμές, ως εξής: (1 + 2 + 3) Χ 3 = 6 Χ 3 = 18. Οπότε, αν μας ρωτήσουν πόσα τρίγωνα περιλαμβάνονται στο σχήμα αυτό, θα απαντήσουμε 18 τρίγωνα.
Σχήμα 12ο
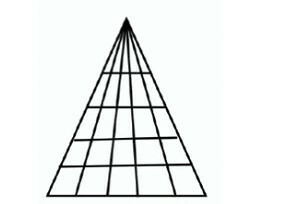
Αυτό το σχήμα δεν μπορεί να μας τρομάξει πλέον, γιατί έχουμε μάθει τον τρόπο επίλυσής του. Μετράμε τα τρίγωνα στη βάση, τα οποία είναι 5 τρίγωνα και τα οποία χωρίζονται 5 φορές μετρώντας τις κάθετες γραμμές, αρχίζοντας να μετράμε από τη βάση. Άρα, τα προσθέτουμε και τα πολλαπλασιάζουμε με το 5 ως εξής: (1 + 2 + 3 + 4 + 5) Χ 5 = 15 Χ 5 = 75 τρίγωνα.
Σχήμα 13ο
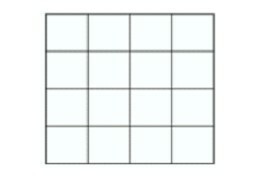
Για να μετρήσουμε τα τετράγωνα, πρώτα προσδιορίζουμε τον τύπο του σχήματος: αν είναι ένα τυπικό πλέγμα όπως εδώ, προσδιορίζουμε τον αριθμό των σειρών και των στηλών. Ο συνολικός αριθμός των τετραγώνων είναι το άθροισμα των τετραγώνων των αριθμών από 1 έως n, δηλαδή εδώ: 1^2 + 2^2 + 3^2 + 4^2 = 1 + 4 + 9 + 16 = 30. Οπότε, εδώ, αν μας ρωτήσουν πόσα τετράγωνα περιλαμβάνονται στο συγκεκριμένο σχήμα, θα απαντήσουμε 30 τετράγωνα.
Σχήμα 14ο
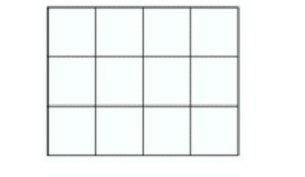
Σε αυτό το σχήμα, ωστόσο, δεν είναι ίσος ο αριθμός των στηλών με των γραμμών. Εδώ κάνουμε άλλο υπολογισμό, και το μόνο σίγουρο είναι ότι δεν μετράμε σχήματα. Έχουμε 3 γραμμές και 4 στήλες και, ακολουθώντας τον εξής τύπο, βρίσκουμε τα τετράγωνα που περιλαμβάνονται ως εξής: (3 Χ 4) + (3-1)(4-1) + (3-2)(4-2) + (3-3)(4-3)= 12 + 6 + 2 + 0 = 20 τετράγωνα.
Σχήμα 15ο
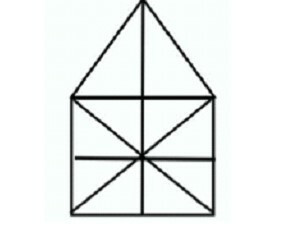
Πάμε να δούμε και αυτό το σχήμα, που τώρα πλέον γνωρίζουμε πως να το υπολογίζουμε, αν μας ζητηθούν πόσα τρίγωνα περιλαμβάνονται. Ξεκινάμε με το κάτω σχήμα, το τετράγωνο, όπου μετράμε 8 τρίγωνα και 2 διαγώνιους, οπότε έχουμε: 8 Χ 2 = 16 τρίγωνα και πάνω έχουμε το γνωστό τρίγωνο, όπου έχουμε 2 τρίγωνα που τα προσθέτουμε μεταξύ τους, οπότε: 1 + 2 = 3. Επομένως, έχουμε 19 (16 + 3) και 2 τα συνδυαστικά τρίγωνα που δημιουργούνται λόγω των δύο σχημάτων αν παρατηρήσετε, τότε έχουμε 21 τρίγωνα ως σωστή απάντηση.
Πάμε τώρα να δούμε πόσα είναι τα τρίγωνα στο σχήμα που έπεσε στον 31ο Εισαγωγικό Διαγωνισμό της ΕΣΔΔΑ με όσα μάθαμε παραπάνω:

Έχουμε 3 σχήματα τα οποία έχουν 8 τρίγωνα το καθένα (4 τρίγωνα Χ 2 διαγώνιους), οπότε για τα τρία σχήματα προσθέτουμε 8 + 8 + 8 = 24 τρίγωνα. Πάμε τώρα στο σχήμα που δεν έχει καθόλου τρίγωνα στη δεξιά κάτω γωνία και πάμε να δούμε πόσα τρίγωνα δημιουργούνται συνδυαστικά με τα υπόλοιπα τρία σχήματα, και αυτά τα μετράμε ως 6 τρίγωνα ακόμα. Οπότε, η σωστή απάντηση ήταν η Γ, δηλαδή 30 τρίγωνα (24 + 6).
Εύκολο;



























